6.7. Backtracking Algorithms: 8 Queens

6.7.1. Problem Description

The queen is one of the most powerful pieces on a chessboard. It can attack anything in its row, or column, or any of its diagonals.

Here are some examples of queens placed on a chess board. The squares in red show the squares the queen can attack.

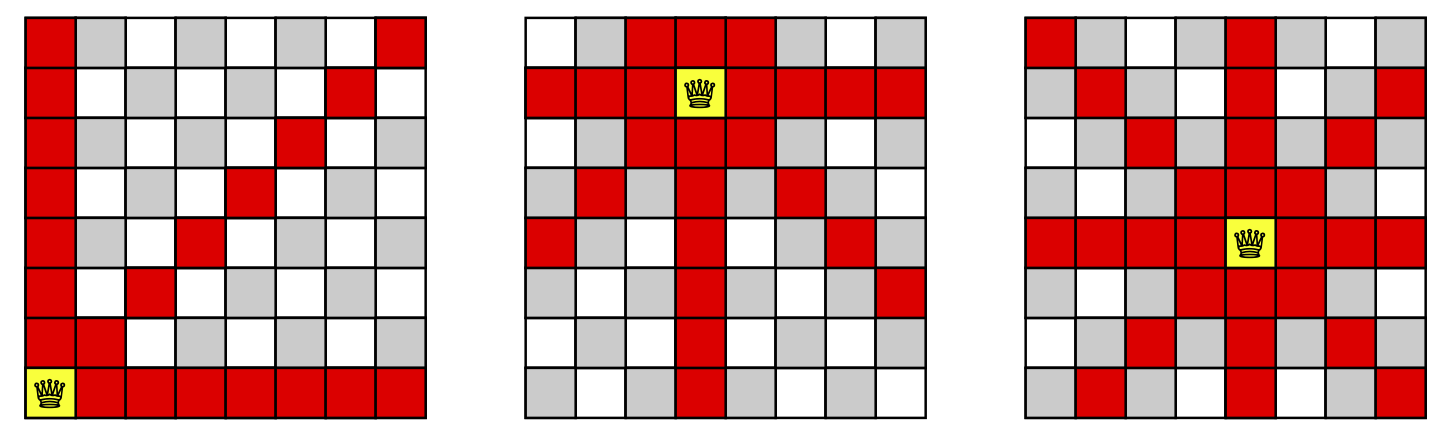
The 8 queens problem is the problem of trying to get 8 queens on the same chessboard without these queens attacking each other. We’ll look at solving this via backtracking.

6.7.2. 4 Queens Problem

For demonstrative purposes, let’s apply the backtracking approach to the ‘4 queens problem’ i.e. can you get 4 queens on a chessboard with the queens attacking.

Recall that backtracking algorithms require repeating the following steps until a solution has been reached.

• Explore. Choose a next step towards a solution.

• Decision. Note if a decision has been made.

• Validate. Check whether the current solution (or partial solution) is valid or whether you’ve reach a complete solution.

• Backtrack. If the solution is not valid, backtrack to the most recent decision where there are still explorable options.

Let’s start with a 4x4 board. Since we know that each queen has to be in a different row, we’ll simplify this problem a little bit and allocate each queen a row. We’ll use the row number to refer to each queen, i.e. queen 1, …, queen 4.

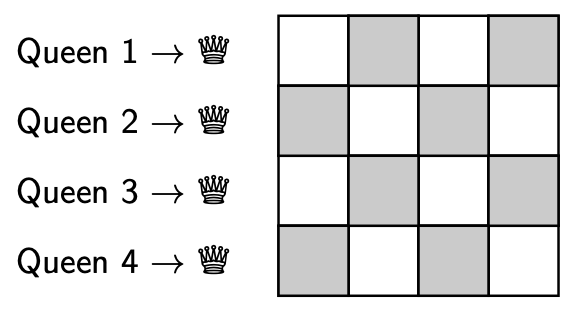
At each step we will carry out the 4 backtracking steps.

• Explore. Explore solutions by changing the board configuration.

• Decision. We need to decide which queen to move and where to move it to. For simplicity we’ll always try to add the next lowest-numbered queen and always try to put them in the left-most column. When a decision has been made we’ll keep track of it by highlighting the decision point (start) in yellow.

• Valid. This is a valid configuration since no queen is attacking another queen on the board.

• Backtrack. N/A, since configuration is valid.

This is now the state of our board.

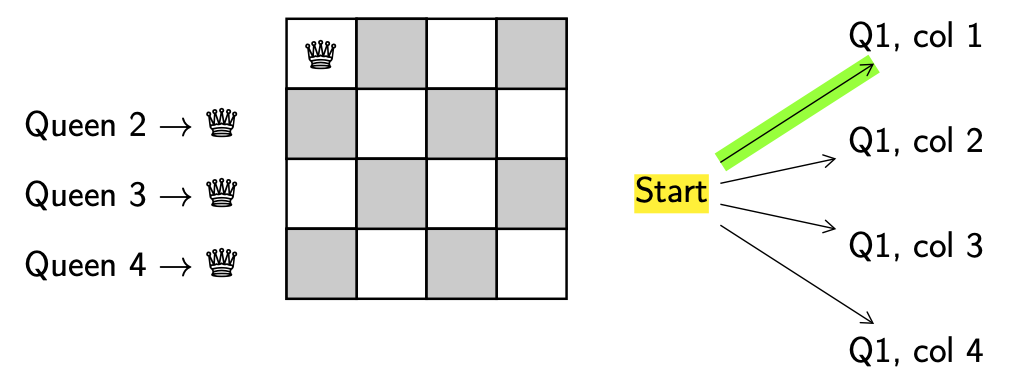
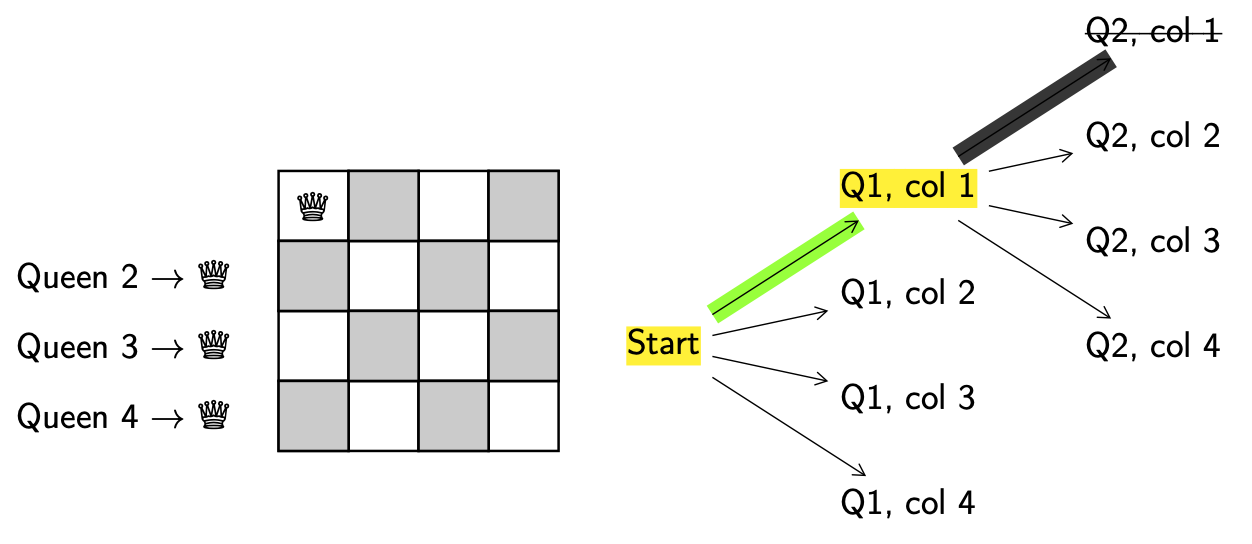
• Explore. Get a new configuration.

• Decision. Put queen 2 (Q2) in column 1 (col 1), since we always try to add the next lowest queen, and put them in columns from left to right. Highlight the decision point (Q1, col 1) in yellow.

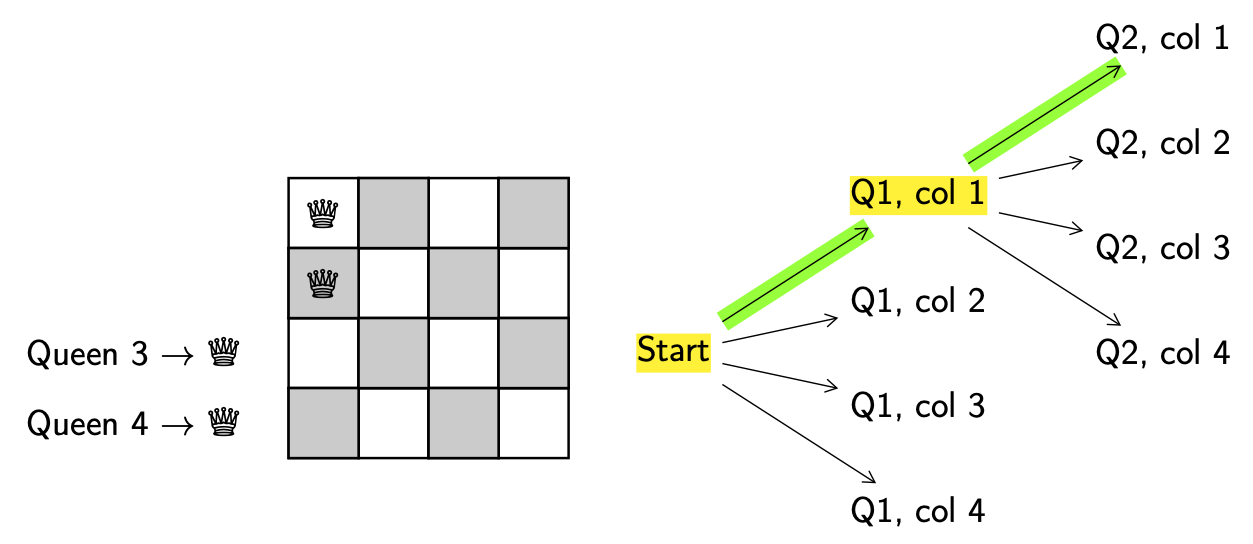
• Valid. No, since queen 1 and 2 are in the same column, they can attack each other.

• Backtrack. Return to the last decision point (Q1, col 1).

We keep going.

• Explore. Get a new configuration.

• Decision. Put queen 2 in column 2.

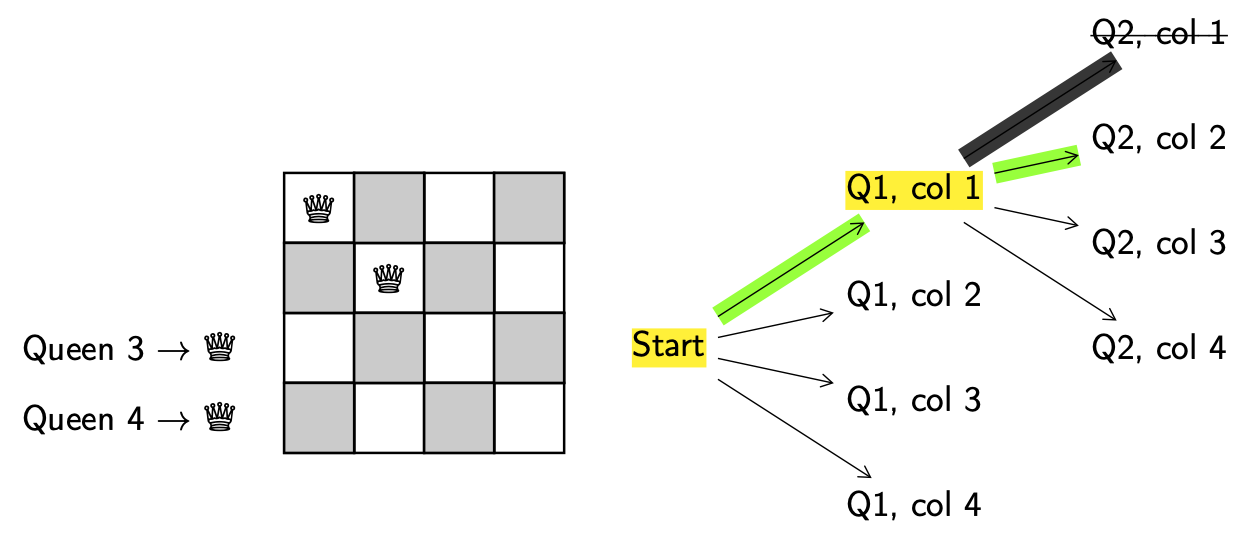
• Valid. No, since queen 1 and 2 are in the same diagonal, they can attack each other.

• Backtrack. Return to the last decision point (Q1, col 1).

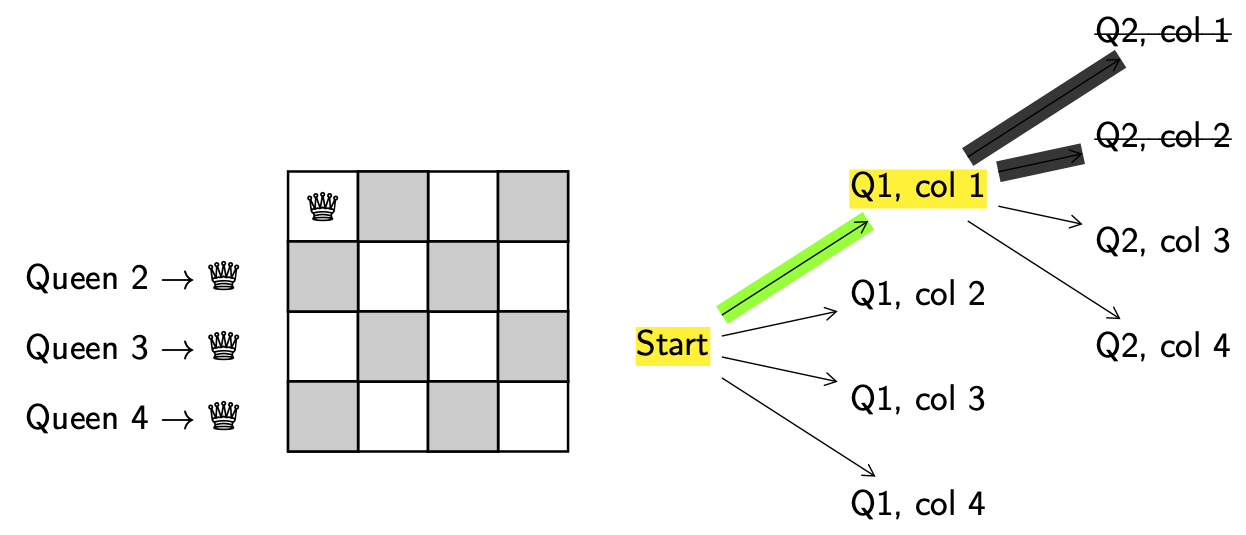
We keep going.

• Explore. Get a new configuration.

• Decision. Put queen 2 in column 3.

• Valid. Yes.

• Backtrack. N/A.

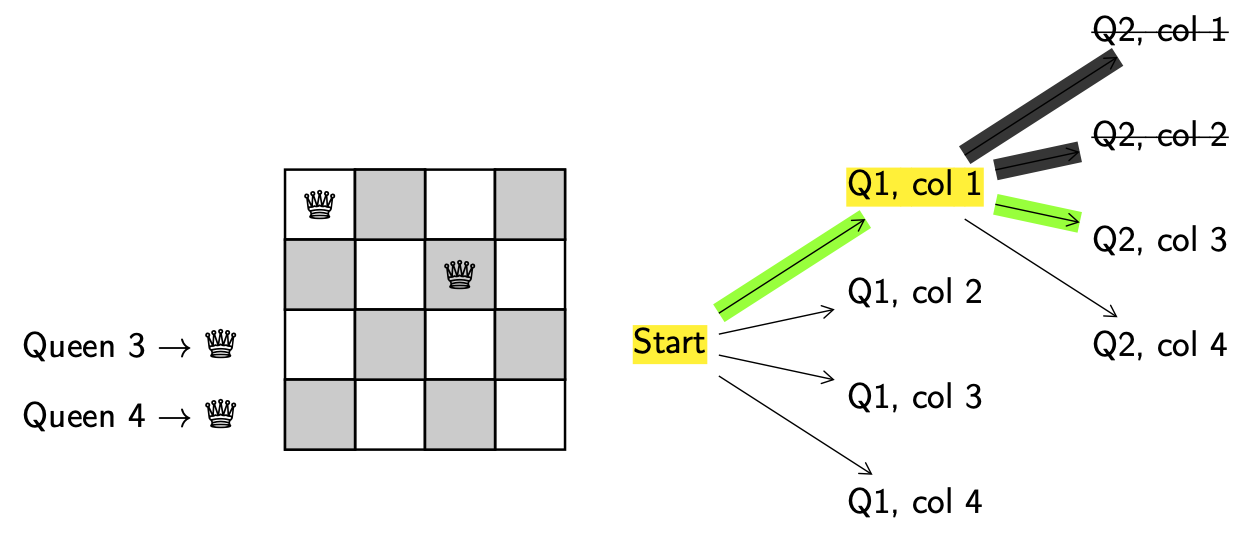
We keep going.

• Explore. Get a new configuration.

• Decision. Put queen 3 in column 1.

• Valid. No, since queen 1 and 3 are in the same column, they can attack each other.

• Backtrack. Return to the last decision point (Q2, col 3).

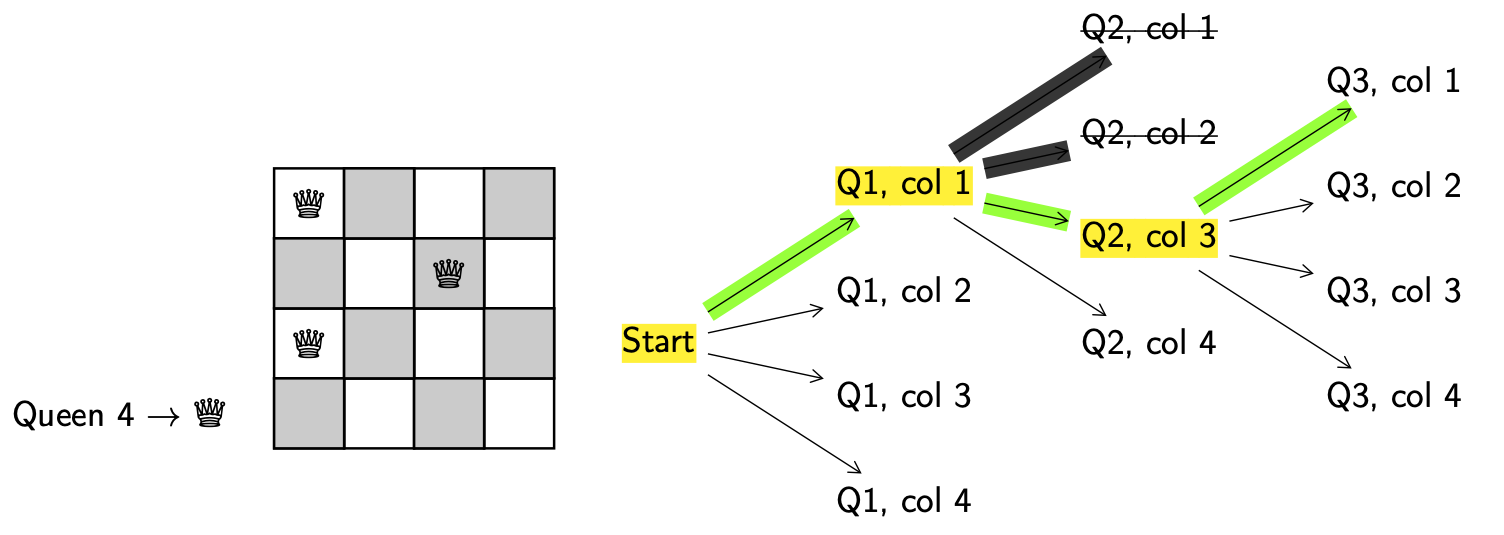
We keep going.

What you’ll probably have notices is that putting queen 3 on the board in column 1, 2, 3 or 4 results in invalid configurations. We consider this a metaphorical dead end.

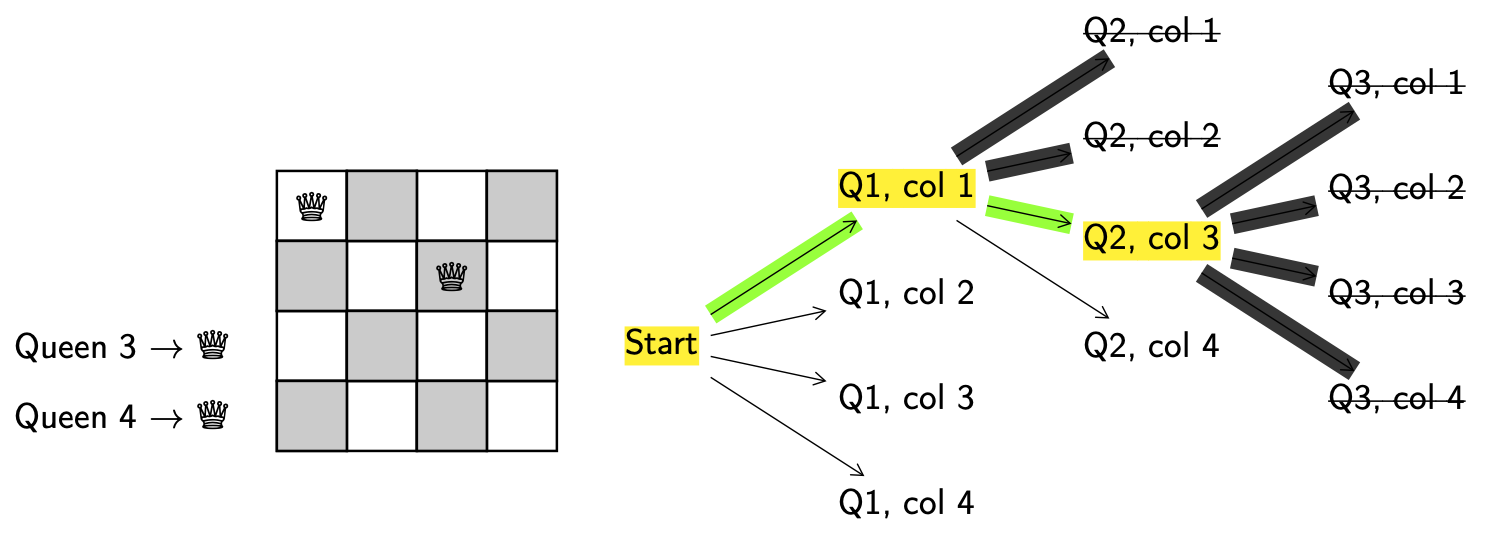
This means we now need to backtrack further all the way back to decision point (Q1, col 1).

We keep going.

• Explore. Get a new configuration.

• Decision. Put queen 2 in column 4.

• Valid. Yes.

• Backtrack. N/A.

We keep going.

• Explore. Get a new configuration.

• Decision. Put queen 3 in column 1.

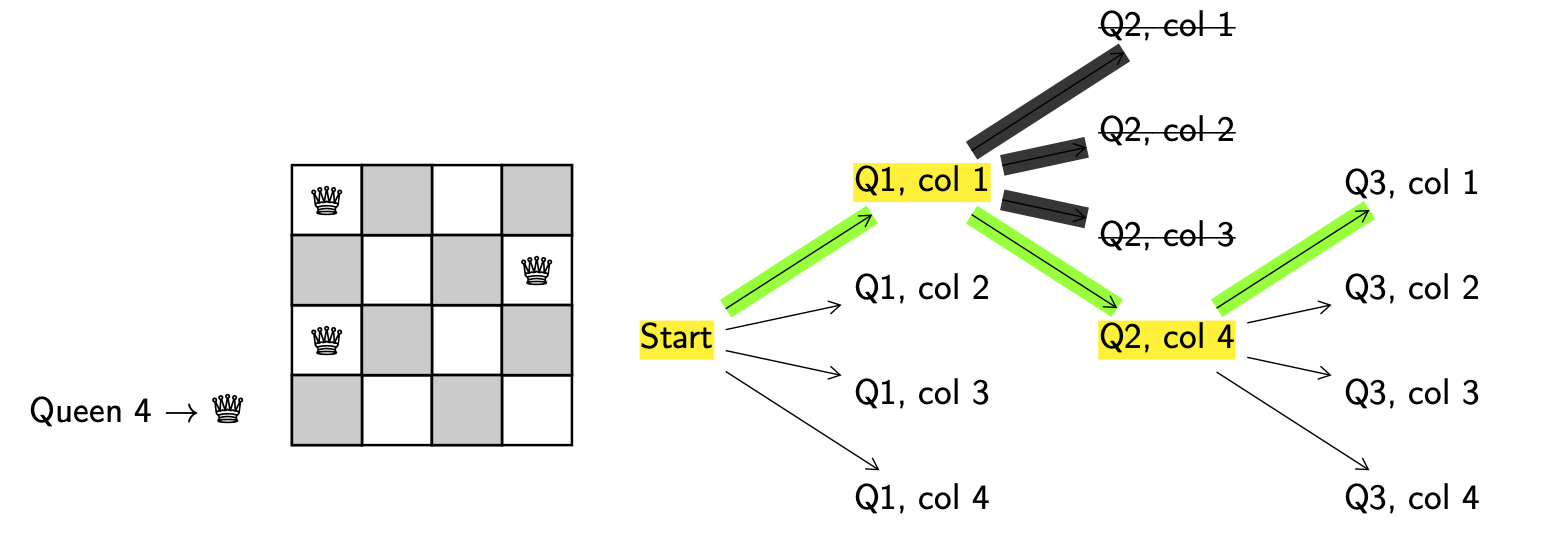
• Valid. No, since queen 1 and 3 are in the same column, they can attack each other.

• Backtrack. Return to the last decision point (Q2, col 4).

We keep going.

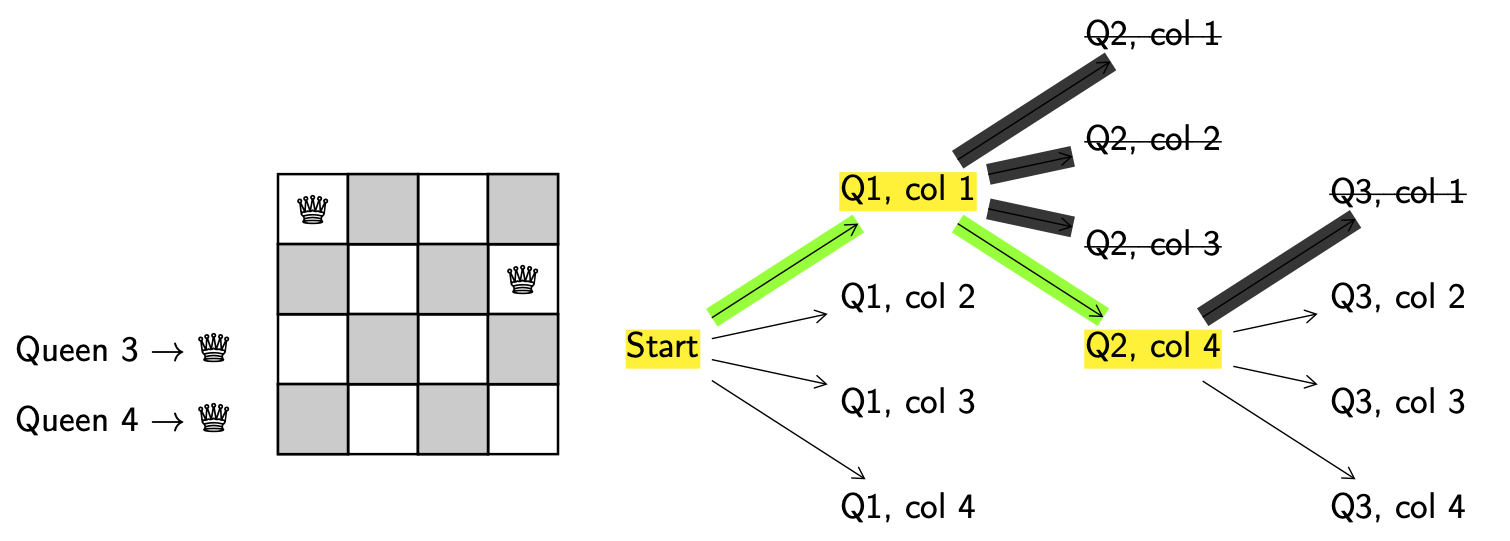
• Explore. Get a new configuration.

• Decision. Put queen 3 in column 2.

• Valid. Yes.

• Backtrack. N/A.

We keep going.

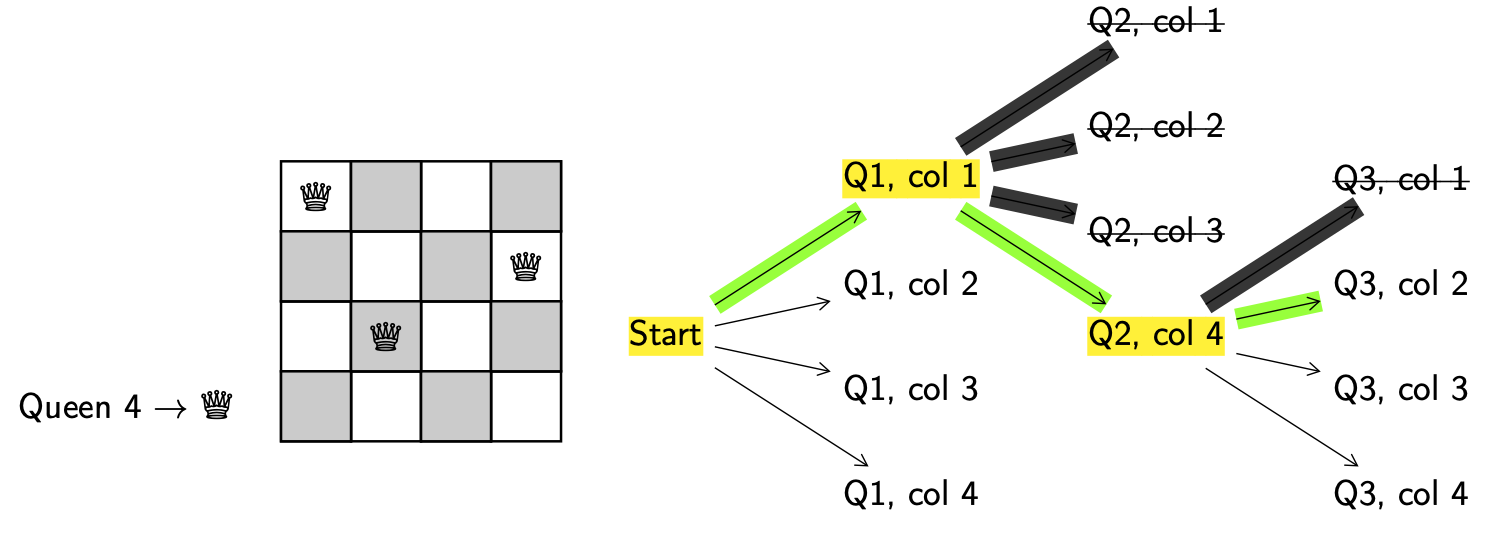
• Explore. Get a new configuration.

• Decision. Put queen 4 in column 1.

• Valid. No, since queen 1 and 4 are in the same column, they can attack each other.

• Backtrack. Return to the last decision point (Q3, col 2).

We keep going.

What you’ll probably have notices is that putting queen 4 on the board in column 1, 2, 3 or 4 results in invalid configurations. We are at another dead end. This means we now need to backtrack further all the way back to decision point (Q2, col 4).

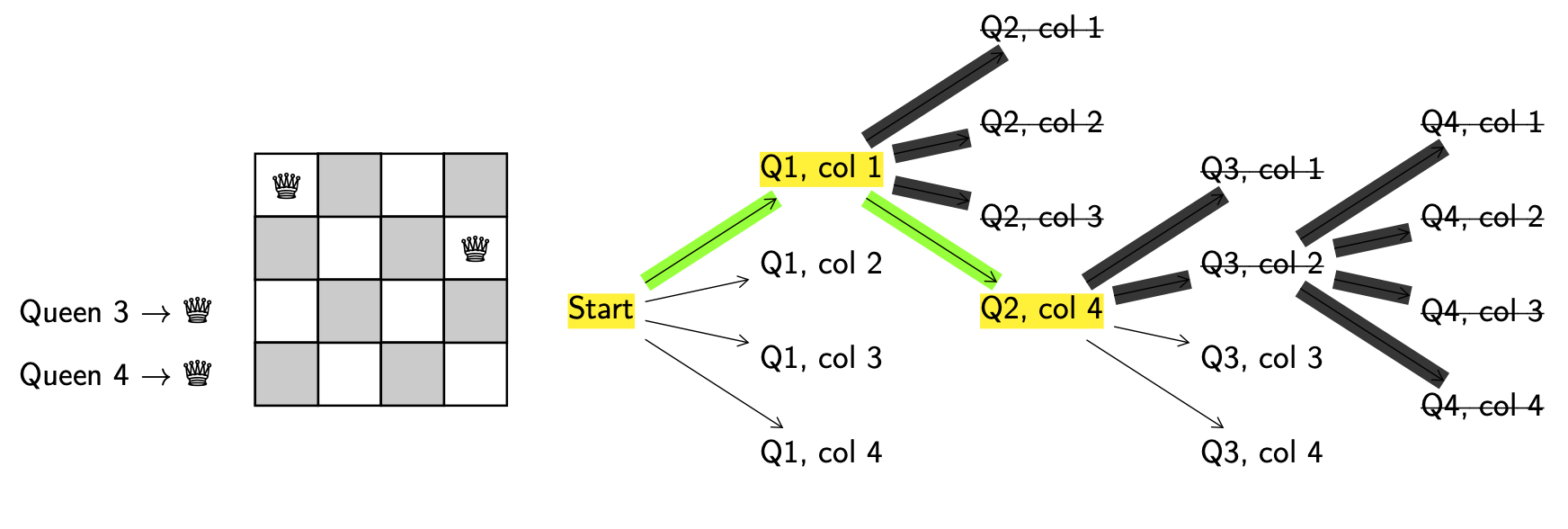
We keep going.

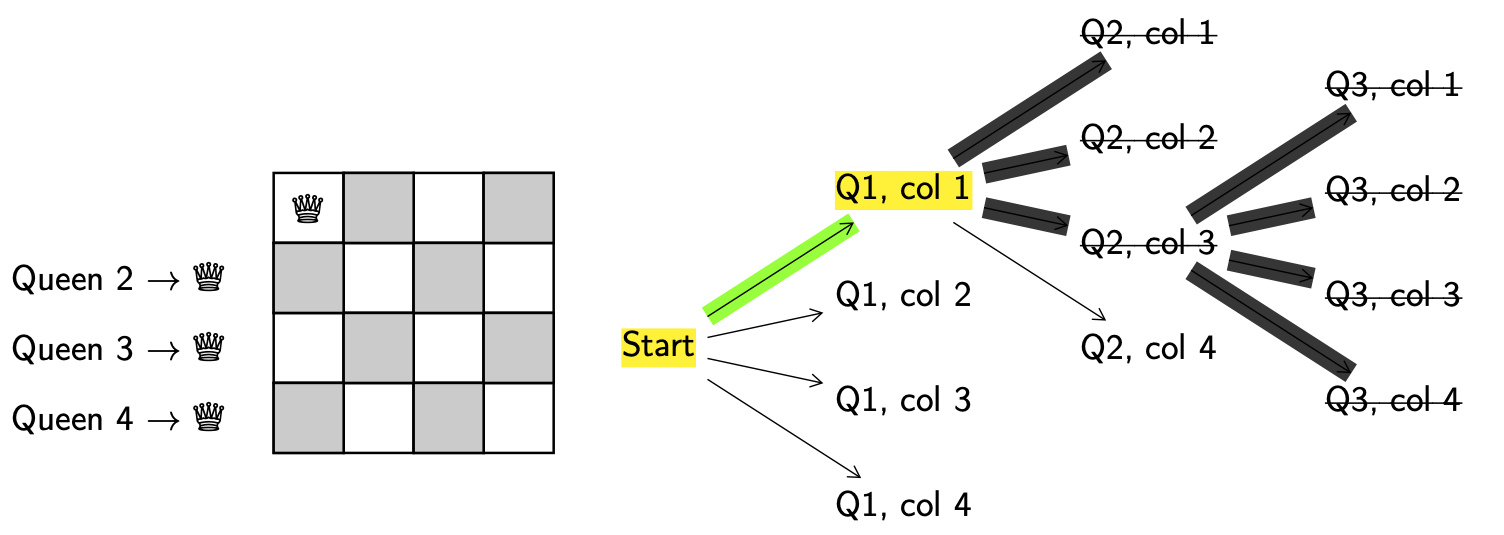
What you’ll probably have notices is that putting queen 3 on the board in column 3 or 4 results in invalid configurations. We are at another dead end! This means we now need to backtrack further all the way back to decision point (Q1, col 1).

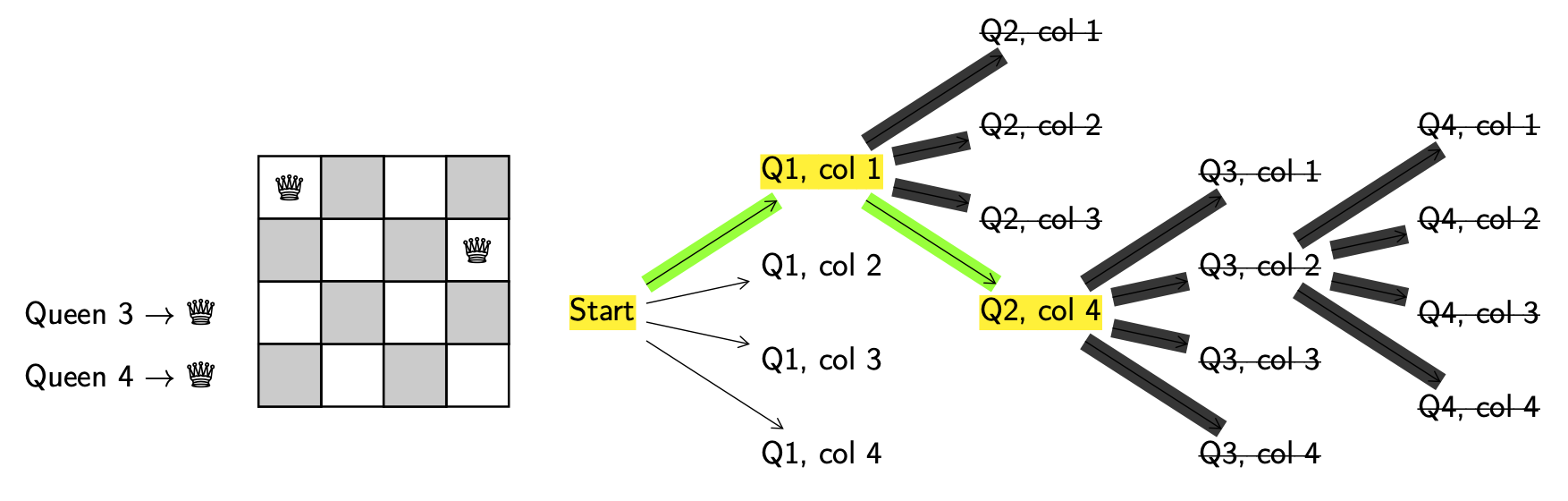
From (Q1, col 1) we are out of options again!

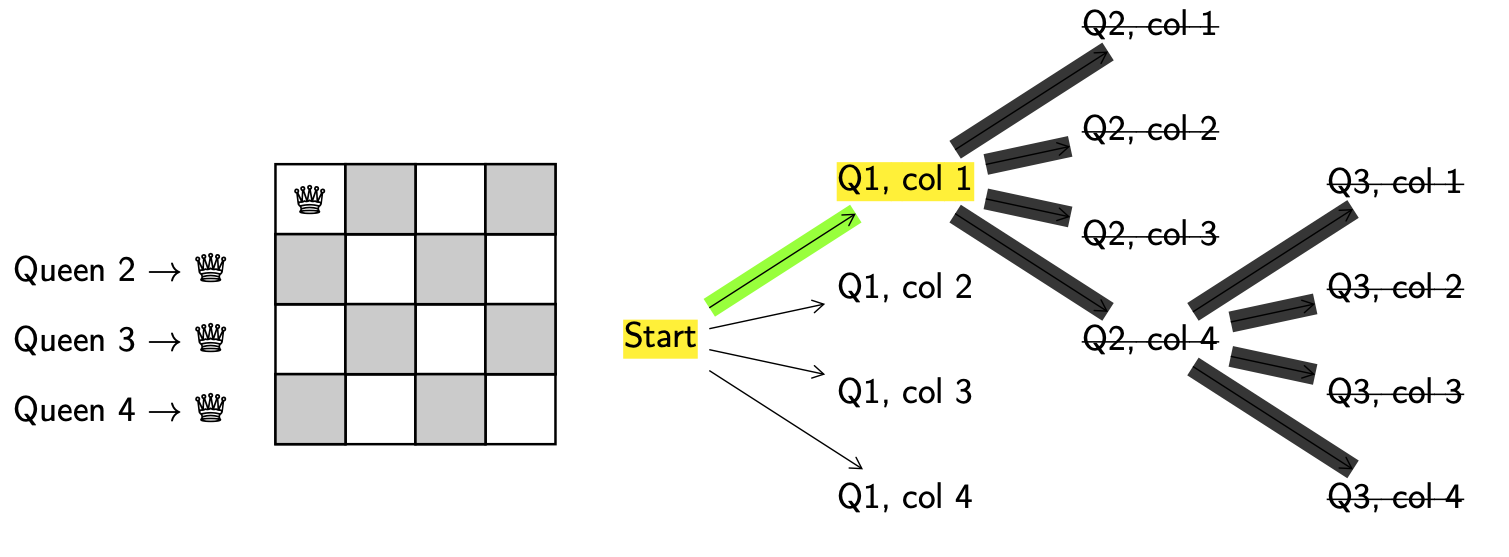
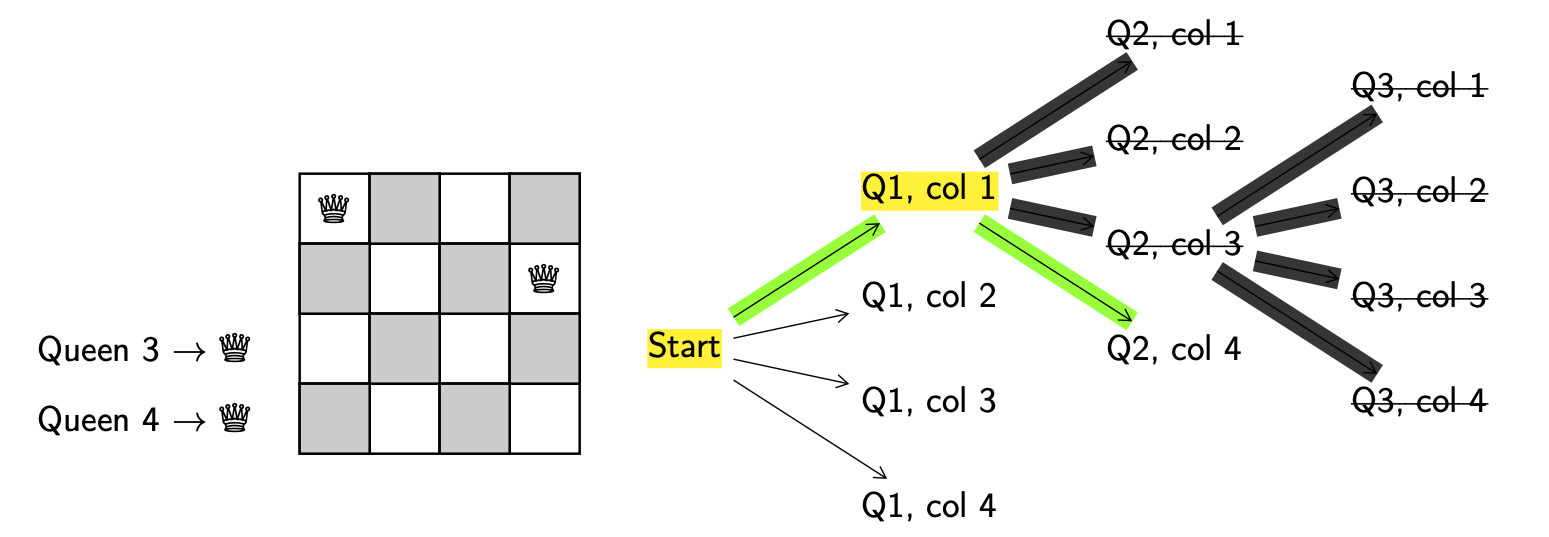
This means we need to backtrack all the way to the start!

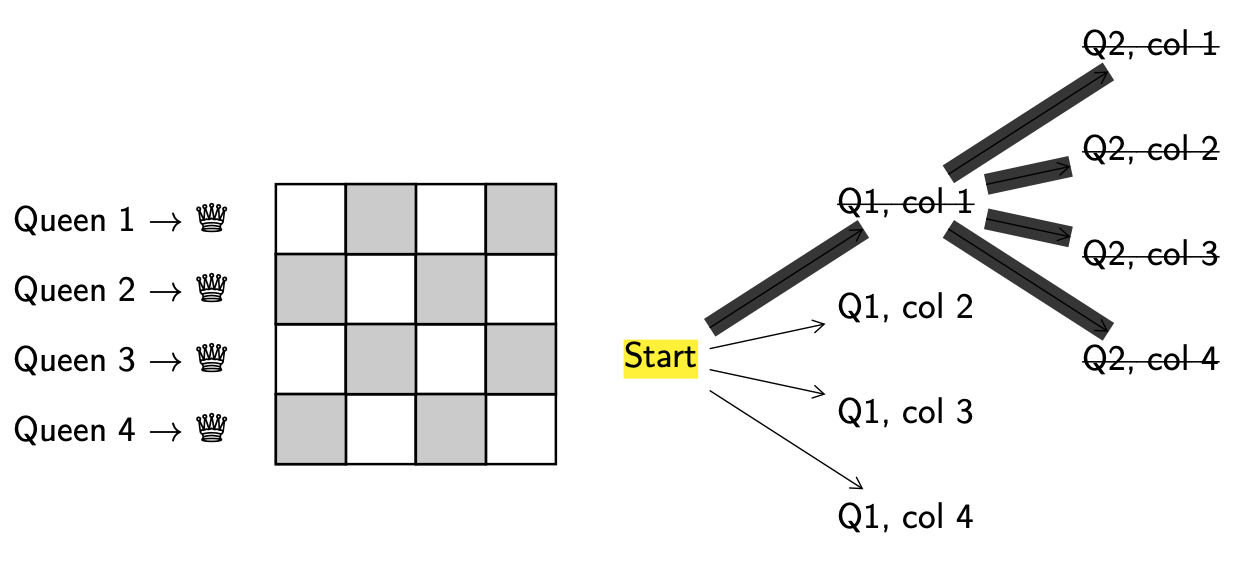
We keep going.

• Explore. Get a new configuration.

• Decision. Put queen 1 in column 2.

• Valid. Yes.

• Backtrack. N/A.

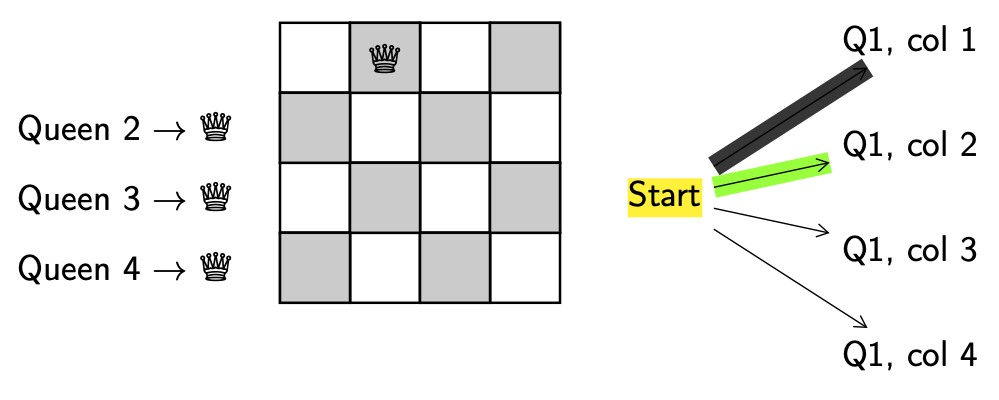
We keep going.

• Explore. Get a new configuration.

• Decision. You’ll notice that the only valid position for queen 2 is in column 4. So skipping a few steps here, lets put queen 2 in column 4.

• Valid. Yes.

• Backtrack. N/A.

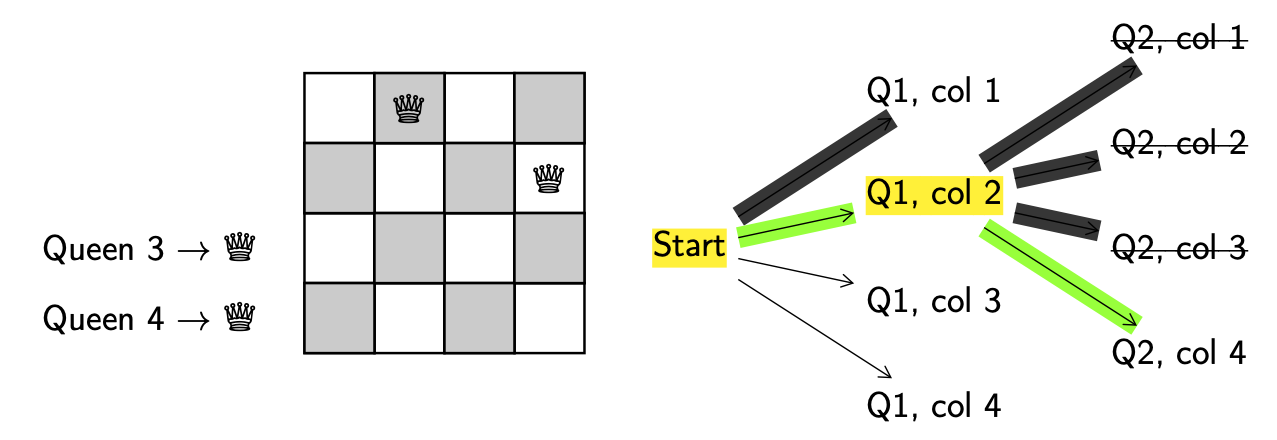
We keep going.

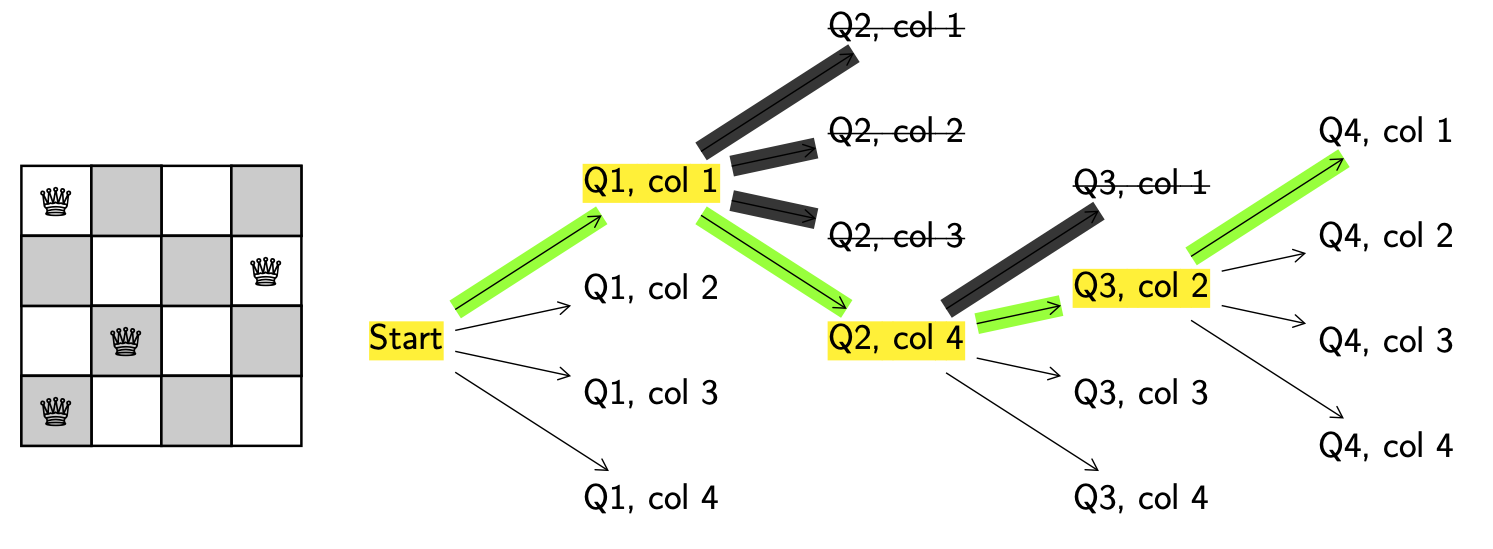
• Explore. Get a new configuration.

• Decision. Put queen 3 in column 1.

• Valid. Yes.

• Backtrack. N/A.

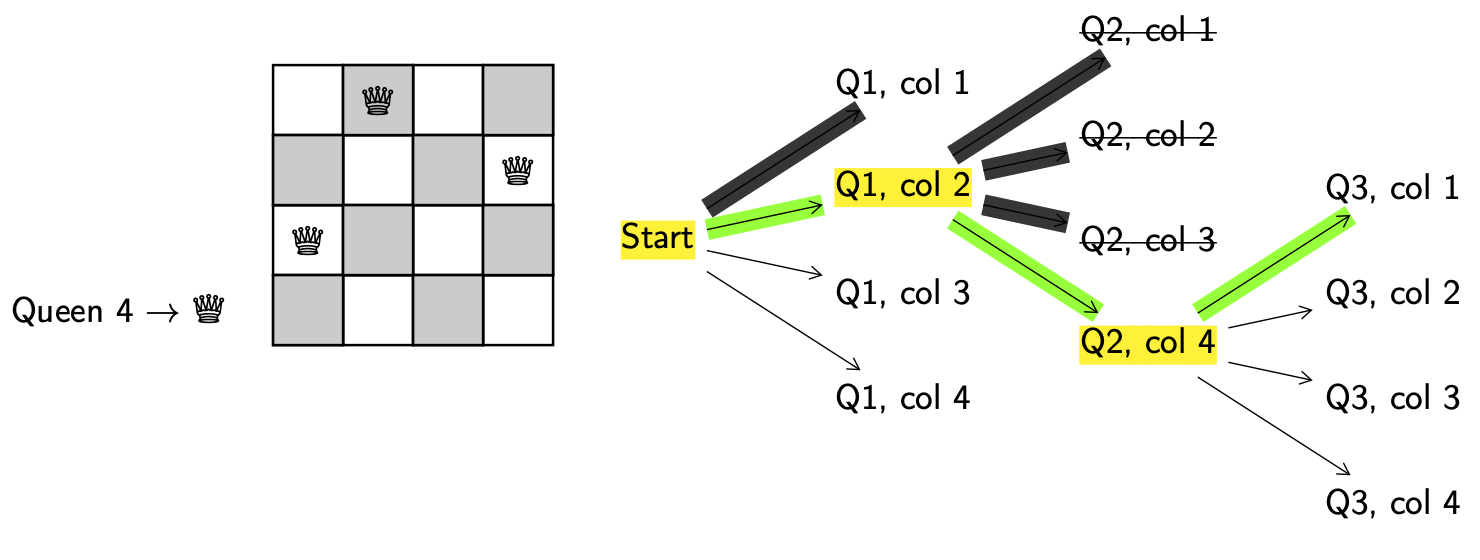
We keep going.

• Explore. Get a new configuration.

• Decision. You’ll notice that the only valid position for queen 4 is in column 3. So skipping a few steps here, lets put queen 4 in column 3.

• Valid. Yes.

• Backtrack. N/A.

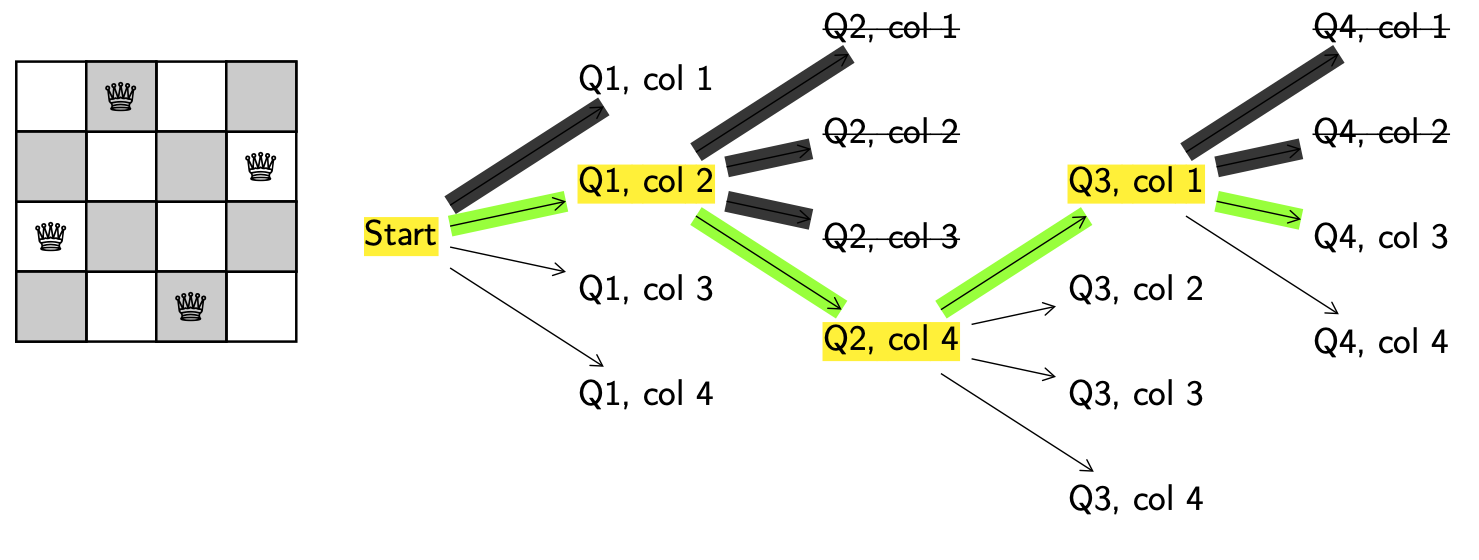
Now we’ve got all the queens on the board and it’s valid! This means we are done!

But you should double check the solution! Make sure no queens can attack by being in the same:

• Row

• Column

• Positive diagonal (bottom left to top right)

• Negative diagonal (top left to bottom right)

Now you can try solving the 8 queens problem yourself!