6.6. Backtracking Algorithms: Maze Example

Backtracking algorithms are a class of algorithms that solve problems by taking the following approach:

Attempt to reach a solution. If it becomes apparent that you’re going down the wrong path, backtrack to the previous decision point, make a different decision and try again. Keep trying until you reach a solution or all possibilities have been explored.

Backtracking algorithms require repeating the following steps until a solution has been reached.

1. Explore. Choose a next step towards a solution.

2. Decision. Note if a decision has been made.

3. Validate. Check whether the current solution (or partial solution) is valid or whether you’ve reach a complete solution.

4. Backtrack. If the solution is not valid, backtrack to the most recent decision where there are still explorable options.

6.6.1. Maze Example

Let’s try and solve a maze using the backtracking algorithm. Consider the following maze.

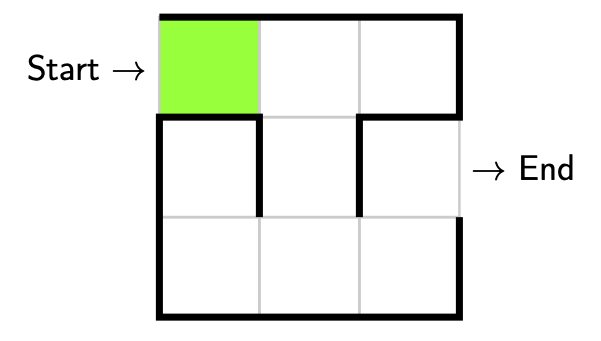
First we explore the maze. Starting at the indicated start we only have one option and that is to take a step forwards. Here we have explored, no decision was made, our partial solution is valid (since we’re not at a dead end), so there is no need to backtrack.

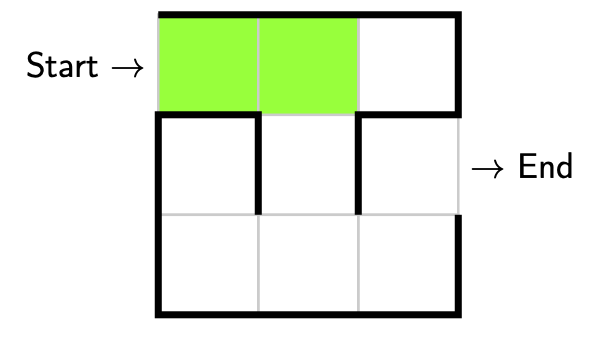
Let’s take another step. Again we only have one option, and that is to take a step forwards. Here we have explored, no decision was made, our partial solution is valid (since we’re not at a dead end), so there is no need to backtrack.

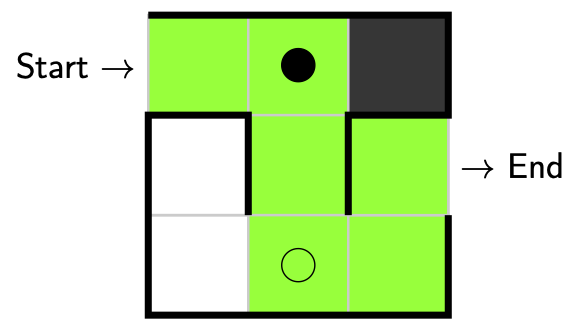
Now we’ll take another step. This time we have two options. We can either go straight ahead or we can go right. Suppose we went straight ahead. Again we have explored, but this time a decision was made! What we’ll do is we’ll place an empty circle to mark down where the decision was made. We also check whether our solution is valid. Unfortunately we have reached a dead end so our solution is not valid.

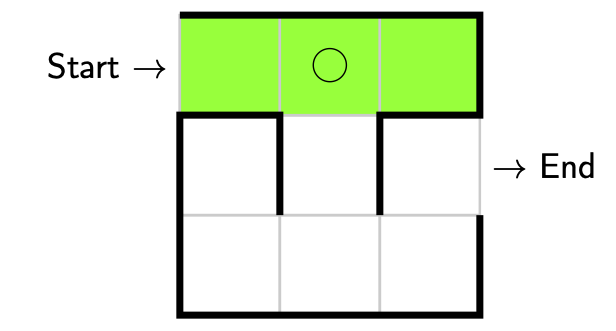
This means we need to backtrack to our most recent decision point where a decision can still be made, i.e. an empty circle.

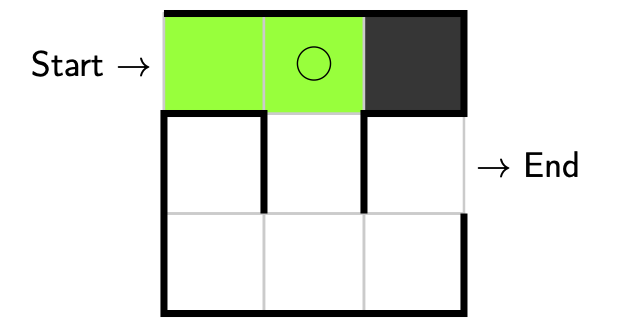
This time we’ll make a different decision and this time turn right. Since this is the last decision we can make from this point there is no need to return here to make a different decision. To indicate this we’ll colour our marker in to remind us not to return. Here we have explored, no decision was made, our partial solution is valid (since we’re not at a dead end), so there is no need to backtrack.

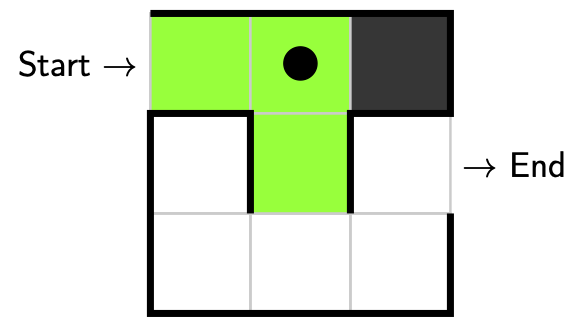
Let’s take another step. Again we only have one option, and that is to take a step forwards. Here we have explored, no decision was made, our partial solution is valid (since we’re not at a dead end), so there is no need to backtrack.

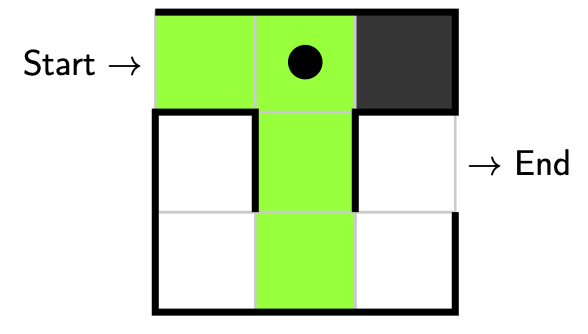
We’ve reached another decision point! We can either go left or we can go right. Suppose we went left. Again we have explored, but since a decision was made we’ll place a little marker down to remind us where the decision was made. We also check whether our partial solution is valid, which is is (since we’re not at a dead end), so there is no need to backtrack.

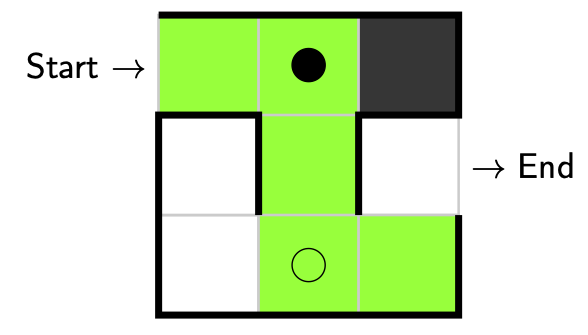
Let’s take another step. Again we only have one option, and that is to take a step forwards. Here we have explored and no decision was made, but this time we can see our solution is valid and complete! We’re done! We’ve solved the maze!